

Schrödinger equation with time-dependent boundary conditions is addressed. The problem of controllability, the problem of existence of solutions for the
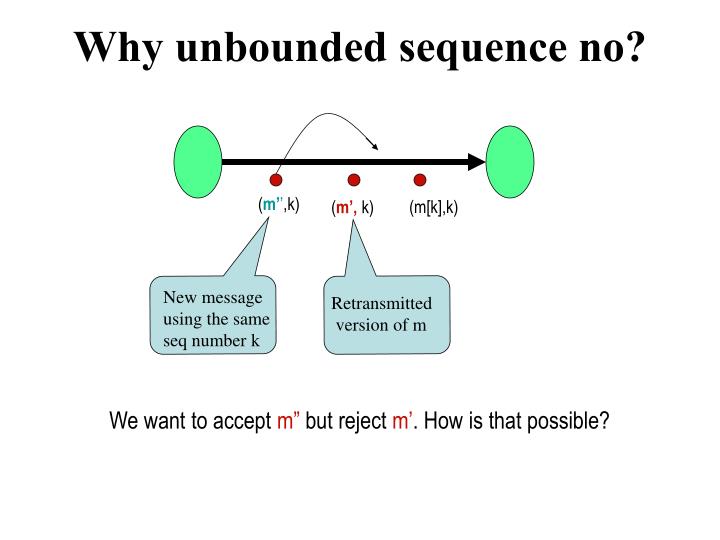
Generalization of quantum grahs) is introduced. Method, a family of boundary control systems on Quantum Circuits (a For showing the viability of the Quantum Control at the Boundary Which makes one to expect that it may help maintaining the quantumĬorrelations. Manipulation and, eventually, its control. Hence, a modification of suchīoundary conditions modifies the state of the system allowing for its On the boundary conditions imposed on it.

Spectrum of a quantum system, for instance an electron moving in a box, depends Quantum system by directly interacting with it through an external field, theĬontrol is achieved by manipulating the boundary conditions of the system. The Quantum Control at the Boundary approach is Systems need to be kept at very low temperatures and the interactions have toīe performed very fast. System in this way, due to the complications of manipulating a system made ofįew particles while maintaining the quantum correlations. Some technological difficulties appear when controlling a quantum The standardĪpproach to quantum control bases on the use of an external field to manipulate
#Quotunbounded control pdf
The construction of this representation is as follows: First, using Steiner selection we parameterize the set-valued map obtained via epigraph of the Legendre–Fenchel conjugate of H.Download a PDF of the paper titled Quantum Control at the Boundary, by Aitor Balmaseda Download PDF Abstract: This dissertation presents and prove the viability of a non-standard methodįor controlling the state of a quantum system by modifying its boundaryĬonditions instead of relying on the action of external fields. Our representation ( A, f, l) of H is an epigraphical representation introduced in. We used a new method to construct a faithful representation. 4, we see that for this type of Hamiltonians there exist faithful representations with the unbounded control set. However, in many cases Hamiltonians do not have bounded Legendre–Fenchel conjugates on effective domains. A necessary condition for the existence of such representations is boundedness of Legendre–Fenchel conjugates of Hamiltonians on effective domains, see. Misztela studied faithful representations of Hamiltonians with the compact control set. In this paper, we provide further developments of representation theorems from.

The triple ( A, f, l), which satisfies the equality ( 4) and inherits Lipschitz-type properties of H, is called a faithful representation of H. There are also irregular representations among them. In general, if a representation of H exists, then infinitely many other representations exist. The triple ( A, f, l), which satisfies the equality ( 4), is called a representation of the Hamiltonian H. In particular, the value function of the optimal control problem given by ( 8) is the unique viscosity solution, see, e.g. It is possible provided that there exists a sufficiently regular triple ( A, f, l) satisfying the equality ( 4). The Hamilton–Jacobi equation ( 6) can be also studied with connection to optimal control problems. The Hamilton–Jacobi equation ( 6) with a convex Hamiltonian H in the gradient variable can be studied with connection to calculus of variations problems, namely the value function of the calculus of variations problem given by ( 7) is the unique viscosity solution, see, e.g.


 0 kommentar(er)
0 kommentar(er)
